1.For PCA, in order to find U and W we need to find a solution to the following objective function:

How can we simplify the equation above such that we transform the problem into a trace maximisation problem? Show the intermediate steps and the new objective function.
Solution:



Now we turn the objective into a trace maximisation problem:


If we define  , this is equivalent (up to a constant factor) to:
, this is equivalent (up to a constant factor) to:

2.With a mean-centered data matrix X, a key component of PCA is the spectral decomposition of a matrix M defined as M= VDVT where:
M ∈Rd,d
V is a matrix whose columns  are the eigenvectors of M
are the eigenvectors of M
D is the diagonal matrix with  and
and  is the eigenvalue of
is the eigenvalue of 
Assume that obtaining the square matrix M is computationally expensive. Can you
suggest an alternative method to obtain the eigenvectors of M?
Solution:
Consider  such that
such that 
Suppose v is an eigenvector of K:  for some
for some  .
.
Multiplying the equation by  and using the definition of K we obtain:
and using the definition of K we obtain:

But, using the definition of 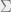 , we get that
, we get that 
Hence  is an eigenvector of
is an eigenvector of 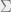 with eigenvalue
with eigenvalue 
Therefore, we can calculate the PCA solution by calculating the eigenvalues of K rather than 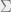 .
.
3.In PCA, W is the compression matrix and U is the recovering matrix. The corresponding objective of finding W and U is phrased as:

Prove the lemma: Let (U,W) be a solution to Objective(1). Then the columns of U are orthonormal (that is,  is the identity matrix of
is the identity matrix of  ) and
) and  .
.
Solution:
Choose any U and W and consider the mapping 
The range of this mapping,  is an r-dimensional linear subspace of
is an r-dimensional linear subspace of  .
.
Let  be a matrix whose columns form an orthonormal basis of this subspace (i.e.
be a matrix whose columns form an orthonormal basis of this subspace (i.e.  ).
).
Each vector in R can be written as  , where
, where  .
.
For every  and
and  we have
we have

This difference is minimised for  .
.
Therefore, for each  we have that:
we have that:

This holds for all  and we can replace U,W by
and we can replace U,W by  without increasing the objective:
without increasing the objective:

As this holds for any U,W, the proof is complete.
4.Let  be the spectral decomposition of
be the spectral decomposition of 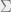 . D is a diagonal matrix, such that
. D is a diagonal matrix, such that  is the i-th largest eigenvalue of
is the i-th largest eigenvalue of 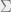 . The columns of V are the corresponding eigenvectors, and
. The columns of V are the corresponding eigenvectors, and  . Then the solution to
. Then the solution to  is the matrix U whose columns are the r first eigenvectors of
is the matrix U whose columns are the r first eigenvectors of 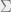 .
.
Solution:
Choose a matrix  with orthonormal columns and let
with orthonormal columns and let  . Then,
. Then,  . It follows that
. It follows that

and therefore
 .
.
Note that  . Hence the columns of B are orthonormal and
. Hence the columns of B are orthonormal and  .
.
Define  to be the matrix such that the first r columns are the columns of B and in addition,
to be the matrix such that the first r columns are the columns of B and in addition,  . Then for every j:
. Then for every j:  , which implies that
, which implies that  .
.
It follows that
![trace(U^T\Sigma U)\leq max_{\beta\in [0,1]^d:\Vert\beta\Vert_1\leq r}\sum^d_{j=1}D_{j,j}\beta_j=\sum^r_{j=1}D_{j,j}](https://s0.wp.com/latex.php?latex=trace%28U%5ET%5CSigma+U%29%5Cleq+max_%7B%5Cbeta%5Cin+%5B0%2C1%5D%5Ed%3A%5CVert%5Cbeta%5CVert_1%5Cleq+r%7D%5Csum%5Ed_%7Bj%3D1%7DD_%7Bj%2Cj%7D%5Cbeta_j%3D%5Csum%5Er_%7Bj%3D1%7DD_%7Bj%2Cj%7D&bg=eeeeee&fg=666666&s=0&c=20201002)
Therefore for every matrix  with orthonormal columns, the following inequality hols:
with orthonormal columns, the following inequality hols: 
But if we set U to the matrix with the r leading eigenvectors of 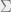 as its columns, we obtain
as its columns, we obtain  and thereby the optimal solution.
and thereby the optimal solution.
5.The variance captured by the first r eigenvectors of  is the sum over its r largest eigenvalues
is the sum over its r largest eigenvalues  .
.
Solution:
The variance in a dataset X is defined as




The variance in a projected dataset WX, with ![W=[\pmb{v}_1,...,\pmb{v}_r]^T](https://s0.wp.com/latex.php?latex=W%3D%5B%5Cpmb%7Bv%7D_1%2C...%2C%5Cpmb%7Bv%7D_r%5D%5ET+&bg=eeeeee&fg=666666&s=0&c=20201002) , is defined as
, is defined as



(Based on 4, we know that the eigenvectors are orthonormal.)
:
. Here
is distributed according to the same distribution as X (
). But this was kind of a big assumption that we can efficiently draw samples from the true distribution P of this random variable X. What happens if we can’t do that? That certainly can happen that we might not be able to draw those samples efficiently.
is our new ‘f(x)’ function, and q(x) is the probability distribution. So we can approximate this by
, and
are drawn according to q before they are drawn according to p.
where
. w is called importance weight.



