Uncategorized – dandan's blog

A singular Value Decomposition is defined as a factorisation of a given matrix $D\in\mathbb{R}^{n\times d}$ into three matrices:

$D=L\Delta R^T$

One can discard the singular vectors that correspond to zero singular values, to obtain the reduced SVD:
$D=L_r\Delta_r R_r^T=\sum^r_{i=1}\delta_i\pmb{l}_i\pmb{r}_i^T$

Eckart-Young Theorem:

If $D_r$ is the matrix defined as $\sum^r_{i=1}\delta_i\pmb{l}_i\pmb{r}_i^T$ , then $D_r$ is the rank-r matrix that minimises the objective $\Vert D-D_r\Vert_F$ .

The Frobenius Norm of a matrix A, $\Vert A\Vert_F$ , is defined as

$\Vert A\Vert_F=\sqrt{\sum^n_{i=1}\sum^n_{j=1}A_{i,j}^2}$

Proof:

Assume D is of rank k(k>r).

Since $\Vert D-D_r\Vert_F=\Vert L\Delta R^T-D_r\Vert_F=\Vert\Delta-L^TD_rR\Vert_F$ .

Denoting $N=L^TD_rR$ , we can compute the Frobenius norm as

$\Vert\Delta-N\Vert^2_F=\sum_{i,j}\vert \Delta_{i,j}-N_{i,j}\vert^2=\sum^k_{i=1}\vert\delta_i-N_{i,i}\vert^2+\sum_{I>k}\vert N_{i,i}\vert^2+\sum_{I\neq j}\vert N_{i,j}\vert^2$

This is minimised if all off-diagonal terms of N and all $N_{i,i}$ for I>k are zero. The minimum of $\sum\vert\delta_i-N_{i,i}\vert^2 is obtained for$ latex N_{i,i} =\delta_i $ for i=1,…,r and all other $N_{i,i}$ are zero.

We do not need the full L and R for computing $D_r$ , only their first r columns. This can be seen by splitting L and R into blocks:

$L=\left[ L_r,L_0 \right]$ and $R=\left[ R_r,R_0\right]$

and

Screen Shot 2018-08-26 at 19.54.41

Classical scaling

The task of MDS is to find the original Euclidean coordinates from a given distance matrix D.

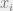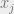The Euclidean distance between the $x_i$ and $x_j$ is given by

$d^2_ij=\sum^d_{k=1}(x_{ik}-x_{jk})^2=(x_i-x_j)^2$

B is the inner-product of dimensional-reduced coordinates. The general $b_{ij}$ term of B is given by

$b_{ij}=\sum^d_{k=1}x_{ik}x_{jk}=x_i^Tx_j$

We can derive B from D:

$d_{ij}^2=x_i^Tx_i+x_j^Tx_j-2x_i^Tx_j=b_{ii}+b_{jj}-2b_{ij}$

For convenient computation, we centre the coordinate matrix X, which implies that $\sum^n_{i=1}b_{ij}=0$ (the sum of the column of B is zero), because the inner product matrix is symmetric, so $\sum^n_{j=1}b_{ij}=0$

Summing over i, we obtain

$\frac{1}{n}\sum^n_{i=1}d_{ij}^2=\frac{1}{n}\sum^n_{i=1}b_{ii}+b_{jj}-\frac{1}{n}\sum^n_{i=1}b_{ij}=\frac{1}{n}\sum^n_{i=1}b_{ii}+b_{jj}$ (59) because $\sum^n_{i=1}b_{ij}=0$

$b_{jj}=\frac{1}{n}\sum^n_{i=1}d^2_{ij}-\frac{1}{n}\sum^n_{i=1}b_{ii}$

Summing over j, we obtain

$\frac{1}{n}\sum^n_{j=1}d^2_{ij}=b_{ii}+\frac{1}{n}\sum^n_{j=1}b_{jj}$ (60)

$b_{ii}=\frac{1}{n}\sum^n_{j=1}d^2_{ij}-\frac{1}{n}\sum^n_{j=1}b_{jj}$

Summing over equation(60), we obtain

$\frac{1}{n}\sum^n_{i=1}(\frac{1}{n}\sum^n_{j=1}d^2_{ij})=\frac{1}{n}\sum^n_{i=1}b_{ii}+\frac{1}{n}\sum^n_{i=1}\frac{1}{n}\sum^n_{j=1}b_{jj}$

$\frac{1}{n^2}\sum^n_{i=1}\sum^n_{j=1}d^2_{ij}=\frac{1}{n}\sum^n_{i=1}b_{ii}+\frac{1}{n}b_{jj}=\frac{2}{n}\sum^n_{i=1}b_{ii}$

We already know that $b_{ij}=-\frac{1}{2}(d^2_{ij}-b_{ii}-b_{jj})$ ;

so $b_{ij}=-\frac{1}{2}(d^2_{ij}-d^2_{i\bullet}-d^2_{\bullet j}+d^2_{\bullet\bullet})$

Define the matrix $\pmb{A}$ as $(a_{ij})$ and observe that:
$\pmb{B}=\pmb{HAH}$

The inner product matrix $\pmb{B}$ can be expressed as

$\pmb{B}=\pmb{XX}^T$

where $X=(\pmb{x}_1,...,\pmb{x}_n)^T$ is the $n\times p$ matrix of coordinates.

The rank of $\pmb{B}$ is then

$rank(\pmb{B})=rank(\pmb{XX}^T)=rank(\pmb{X})=p$

$\pmb{B}$ is symmetric, positive definite, of rank p and has p non-zero eigenvalues.

B can now be written as $\pmb{B}=\pmb{V}_p\pmb{Lambda}_p\pmb{V}_p^T$

where $\pmb{Lambda}_p=diag(\lambda_1,...,\lambda_p)$ , the diagonal matrix of the eigenvalues of B, and $\pmb{V}_p=(\pmb{v}_1,...,\pmb{v}_p)$ , the matrix of corresponding eigenvectors.

Hence the coordinate matrix X containing the point configuration in 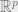$\mathbb{R}^p$ is given by $\pmb{X}=\pmb{V}_p\pmb{\Lambda}_p^{\frac{1}{2}}$

Pseudocode

The algorithm for recovering coordinates from distances $D_{ij}=d_{ij}$ between pairs of points is as follows:

Form matrix $A_{ij}=\left\{ -\frac{1}{2}d_{ij}^2 \right\}$
Form matrix $latex \pmb{B}=\pmb{HAH}$, where H is the cantering matrix $\pmb{H}=\pmb{I}-\frac{1}{n}\pmb{11}^T$
Find the spectral decomposition of B, and V is the matrix of corresponding eigenvectors.
If the points were originally in a p-dimensional space, the first p eigenvalues of K are nonzero and the remaining n-p are zero. Discard these from $\Lambda$ (rename as $\Lambda_p$ ), and discard the corresponding eigenvalues from V (rename as $\pmb{V}_p$ ).
Find $\pmb{X}=\pmb{V}_p\pmb{\Lambda}_p^{\frac{1}{2}}$ , and then the coordinates of the points are given by the rows of X.